
【ADHD血液診断】特徴量を選択してから次元削減
目次
0. はじめに
本記事は、以下の記事の続きになります。
https://www.bioinforest.com/adhd1-3
1. 特徴量をt検定で絞る
モデル作成に用いる特徴量の選定に、群の間で差がある特徴量を利用することが多々あります。
今回は、ライブラリをimportし、t検定で特徴量を絞ります。
Text
import timeimport pickle
import pandas as pdimport numpy as np
import matplotlib.pyplot as pltimport seaborn as sns
from scipy.stats import pearsonrfrom sklearn.decomposition import PCAfrom sklearn.manifold import TSNEimport umapfrom scipy.sparse.csgraph import connected_components
import scipy.stats as stfrom scipy.stats import mannwhitneyu
import warningswarnings.filterwarnings('ignore')
df_ctrl = df_rep[df_rep["y"]==0]df_adhd = df_rep[df_rep["y"]==1]
ps = []
shapiro_ctrl = df_ctrl.apply(lambda x: st.shapiro(x)[1]).tolist()[:-1]shapiro_adhd = df_adhd.apply(lambda x: st.shapiro(x)[1]).tolist()[:-1]
for i in range(df_ctrl.shape[1]-1):
if shapiro_ctrl[i] > 0.05 and shapiro_adhd[i] > 0.05:
if st.levene(df_ctrl.iloc[:,i], df_adhd.iloc[:,i],center='mean')[1] > 0.05: p = st.ttest_ind(df_ctrl.iloc[:,i], df_adhd.iloc[:,i], equal_var=True)[1]
else: p = st.ttest_ind(df_ctrl.iloc[:,i], df_adhd.iloc[:,i], equal_var=False)[1]
else: p = mannwhitneyu(df_ctrl.iloc[:,i], df_adhd.iloc[:,i], alternative='two-sided', use_continuity=True)[1]
ps.append(p)
idxes = [i for i in range(len(ps)) if ps[i] <= 0.01] + [df_rep.shape[1]-1]df_ttest = df_rep.iloc[:, idxes]df_ttest.to_csv("src/df_ttest.csv")df_ttest.shapeText
(76, 2141)2. 標準化
Text
x = df_rep.iloc[:, :-1]x_scaled = (x - x.mean()) / x.std()3. PCA
まずは次元削減を実施し、現在のデータのまま十分にADHDであるか判定できそうか大雑把に調べます。
PCA、tSNE、UMAPの順に試していきます。
Text
pca = PCA()pca.fit(x_scaled)
score = pd.DataFrame(pca.transform(x_scaled), index=x_scaled.index)
plt.scatter(score.iloc[:, 0], score.iloc[:, 1], c=df_xy.iloc[:, -1], cmap=plt.get_cmap('jet'))clb = plt.colorbar()clb.set_label('ADHD Status', labelpad=-20, y=1.1, rotation=0)plt.xlabel('PC1')plt.ylabel('PC2')plt.show()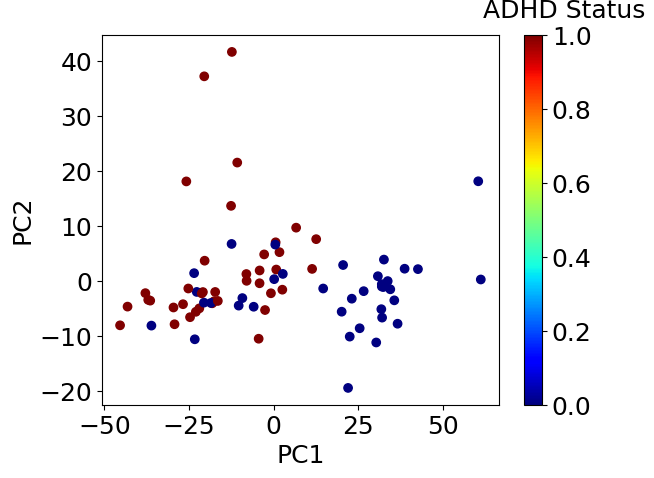
Text
# 寄与率contribution_ratios = pd.DataFrame(pca.explained_variance_ratio_)cumulative_contribution_ratios = contribution_ratios.cumsum()
cont_cumcont_ratios = pd.concat([contribution_ratios, cumulative_contribution_ratios], axis=1).Tcont_cumcont_ratios.index = ['contribution_ratio', 'cumulative_contribution_ratio'] # 行の名前を変更# 寄与率を棒グラフで、累積寄与率を線で入れたプロット図を重ねて描画x_axis = range(1, contribution_ratios.shape[0] + 1) # 1 から成分数までの整数が x 軸の値plt.rcParams['font.size'] = 18plt.bar(x_axis, contribution_ratios.iloc[:, 0], align='center') # 寄与率の棒グラフplt.plot(x_axis, cumulative_contribution_ratios.iloc[:, 0], 'r.-') # 累積寄与率の線を入れたプロット図plt.xlabel('Number of principal components') # 横軸の名前plt.ylabel('Contribution ratio(blue),\nCumulative contribution ratio(red)') # 縦軸の名前。\n で改行していますplt.show()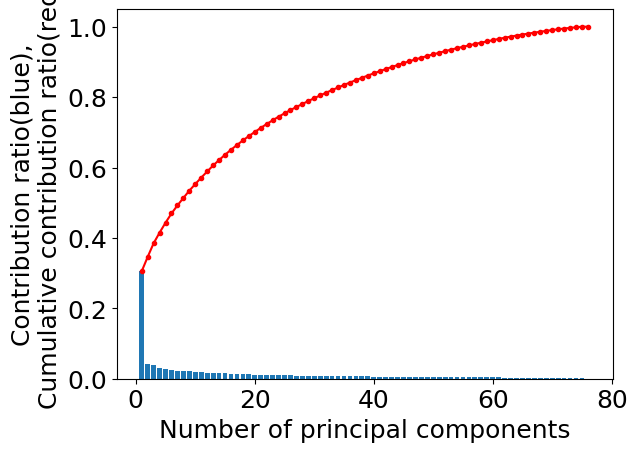
4. tSNE
Text
tsne = TSNE(n_components=2, random_state=42)corrdinates = pd.DataFrame(tsne.fit_transform(x_scaled))
plt.scatter(corrdinates.iloc[:, 0], corrdinates.iloc[:, 1], c=df_xy.iloc[:, -1], cmap=plt.get_cmap('jet'))clb = plt.colorbar()clb.set_label('ADHD Status', labelpad=-20, y=1.1, rotation=0)plt.xlabel('tSNE 1')plt.ylabel('tSNE 2')plt.show()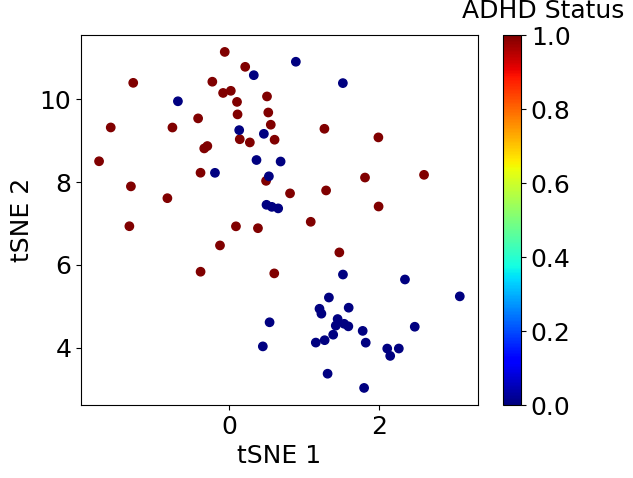
5. UMAP
Text
embedding = pd.DataFrame(umap.UMAP().fit_transform(x_scaled))
plt.scatter(embedding.iloc[:, 0], embedding.iloc[:, 1], c=df_xy.iloc[:, -1], cmap=plt.get_cmap('jet'))clb = plt.colorbar()clb.set_label('ADHD Status', labelpad=-20, y=1.1, rotation=0)plt.xlabel('UMAP 1')plt.ylabel('UMAP 2')plt.show()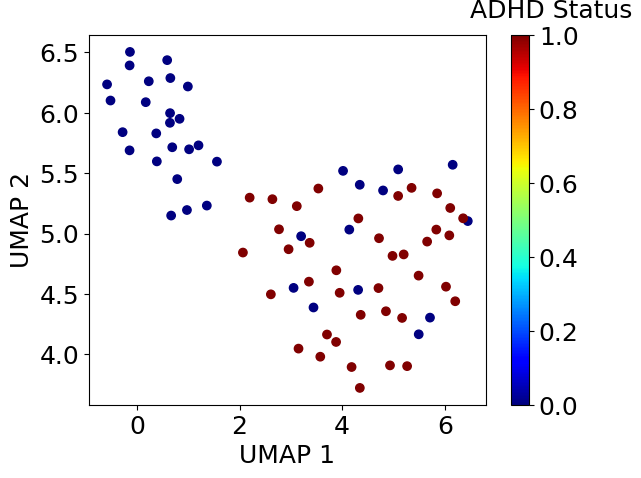
6. まとめ
特徴量を絞ることでUMAPではADHD患者と健常人がかなり明瞭に分かれました。
このデータをベースに機械学習モデルを作成すると良さそうです。

