Forest background
バイオインフォの森へようこそ
【理論/Python実装】Graphical LASSO【遺伝子発現制御】

【理論/Python実装】Graphical LASSO【遺伝子発現制御】

目次

はじめに

**Graphical LASSO（グラフィカルラッソ）**は、多変量正規分布に基づく変数間の条件付き独立性を推定し、スパースなネットワーク構造を復元するための強力な手法です。

特に、高次元データ（変数の数がサンプル数を大きく超えるデータ）において、精度行列（分散共分散行列の逆行列）のスパース推定が重要な課題となります。

本記事では、Graphical LASSOの理論を数式を交えて丁寧に解説し、Pythonによる実装と遺伝子発現制御ネットワークへの応用にも触れます。

1. 多変量正規分布と条件付き独立性

まず、Graphical LASSOが対象とするのは、pp次元の多変量正規分布： (X \sim \mathcal{N}_p(0, \Sigma))です。

ここで、

  • Σ\Sigma は正定値の共分散行列

  • Θ=Σ−1\Theta = \Sigma^{-1} は精度行列（逆共分散行列）

です。

多変量正規分布における重要な性質として： θ_ij=0⟺X_i⊥X_j∣X_∖i,j\theta\_{ij} = 0 \quad \Longleftrightarrow \quad X\_i \perp X\_j \mid X\_{\setminus{i,j}}

が成り立ちます。つまり、精度行列の非ゼロパターンが、変数間の条件付き独立関係を表すのです。

2. 尤度関数の導出

次に、データ X=x_1,x_2,…,x_nX = {x\_1, x\_2, \dots, x\_n} （nnサンプル、pp次元）の対数尤度関数を導出します。

多変量正規分布の確率密度関数は

f(x;Θ)=∣Θ∣1/2(2π)p/2exp⁡(−12x⊤Θx)f(x; \Theta) = \frac{|\Theta|^{1/2}}{(2\pi)^{p/2}} \exp\left( -\frac{1}{2} x^\top \Theta x \right)

です。

これを nn個の独立なサンプル x_1,…,x_nx\_1, \dots, x\_n に対して対数を取ると

ℓ(Θ;X)=∑_i=1n(12log⁡∣Θ∣−12x_i⊤Θx_i)+定数\ell(\Theta; X) = \sum\_{i=1}^n \left( \frac{1}{2} \log |\Theta| - \frac{1}{2} x\_i^\top \Theta x\_i \right) + \text{定数}

となります。

定数項を除いてまとめると

ℓ(Θ;X)=n2log⁡∣Θ∣−n2tr(SΘ)\ell(\Theta; X) = \frac{n}{2} \log |\Theta| - \frac{n}{2} tr(S \Theta)

ここで、SS は標本共分散行列： S=1n∑_i=1nx_ix_i⊤S = \frac{1}{n} \sum\_{i=1}^n x\_i x\_i^\top

です。

3. Graphical LASSOの最適化問題の導出

3.1 最大対数尤度推定（MLE）

LASSOの前に、通常の最大対数尤度推定（MLE）の問題は次の通りです

\max\_{\Theta \succ 0} \ \left{ \log |\Theta| - tr(S \Theta) \right}

これは共分散行列の逆行列を直接推定する問題です。

しかし、高次元（p≫np \gg n）の場合、SSは特異行列であり、直接の推定は不可能です。

3.2 L1正則化の導入（Graphical LASSO）

ここで、スパース性を導入するために、L1正則化を加えます。以下がGraphical LASSOの目的関数です。

\max\_{\Theta \succ 0} \ \left{ \log |\Theta| - tr(S \Theta) - \lambda \sum\_{i \neq j} |\theta\_{ij}| \right}

または最小化形式に書き換えると

\min\_{\Theta \succ 0} \ \left{ -\log |\Theta| + tr(S \Theta) + \lambda |\Theta|\_1 \right}

となります。

ここで∣Θ∣_1=∑_i≠j∣θ_ij∣|\Theta|\_1 = \sum\_{i \neq j} |\theta\_{ij}|は精度行列のオフダイアゴナル要素のL1ノルムです。

4. 式変形の詳細解説

4.1 ログ行列式の性質

まず、行列式の対数は以下のような性質を持ちます。

log⁡∣Θ∣=∑_i=1plog⁡λ_i\log |\Theta| = \sum\_{i=1}^p \log \lambda\_i

ここで、λ_i\lambda\_i は Θ\Theta の固有値です。

精度行列は正定値なので、固有値は全て正です。

4.2 トレースの性質

tr(SΘ)=∑_i,jS_ijθ_jitr(S \Theta) = \sum\_{i,j} S\_{ij} \theta\_{ji}

です。トレースは行列積の要素積の和であり、対称性のある二次形式において重要な役割を果たします。

4.3 正則化項の意味

L1ノルム正則化項λ∑_i≠j∣θ_ij∣\lambda \sum\_{i \neq j} |\theta\_{ij}|は、精度行列の非対角成分（条件付き依存関係を示す部分）のスパース化を促します。

特に、λ\lambdaを大きくすると、多くの要素がゼロ化されます。

4.4 Graphical LASSOの目的関数まとめ

Graphical LASSOの最終的な目的関数は次のようになります。

L(Θ)=−log⁡∣Θ∣+tr(SΘ)+λ∑_i≠j∣θ_ij∣\boxed{ \mathcal{L}(\Theta) = -\log |\Theta| + tr(S \Theta) + \lambda \sum\_{i \neq j} |\theta\_{ij}| }

この問題は、**対数尤度の最大化（モデルのあてはまりの良さ）**と、**L1ノルムによるスパース性の強制（過学習の防止）**のトレードオフを解く問題です。

5. Graphical LASSOの解法

この最適化問題は凸最適化問題であり、Friedmanら（2008）の論文で提案された「ブロック座標降下法」によって解かれます。基本的なアイデアは次の通りです：

  • Θ\Theta の1行1列を固定し、他の行列成分を条件付きで最適化

  • サブ問題はLASSO回帰に帰着し、既存のアルゴリズムで解ける

  • 各変数について反復的に更新

詳細な解法アルゴリズムは専門的な内容になるため、別記事で解説します。

6. Graphical LASSOの意義と応用

Graphical LASSOは、以下のような問題に応用されています：

  • 遺伝子ネットワークの推定

  • 脳神経活動ネットワークの解析（fMRIデータ）

  • 金融市場におけるリスクネットワークの構造推定

  • 気象データやIoTセンサーデータの依存構造解析

特に、**高次元小サンプル問題（p≫np \gg n）**での安定したネットワーク推定が可能な点が強力です。

7. Graphical LASSOのPythonによる実装

Pythonでは、sklearnやskggm、QUICライブラリなどを用いてGraphical LASSOを実装できます。ここでは、sklearn.covarianceモジュールのGraphicalLassoクラスを使った例を紹介します。

7.1 必要なライブラリのインポート

Text
import numpy as np
import matplotlib.pyplot as plt
from sklearn.covariance import GraphicalLasso
import seaborn as sns

7.2 データの生成

まずは、ダミーデータを生成します。

Text
np.random.seed(0)
n_samples, n_features = 100, 5


# 相関構造を持つ共分散行列
prec = np.array([
    [1.0, -0.4, 0, 0, 0],
    [-0.4, 1.0, -0.3, 0, 0],
    [0, -0.3, 1.0, -0.2, 0],
    [0, 0, -0.2, 1.0, -0.1],
    [0, 0, 0, -0.1, 1.0]
])


cov = np.linalg.inv(prec)
X = np.random.multivariate_normal(mean=np.zeros(n_features), cov=cov, size=n_samples)

Xの形状と中身は以下です。

Text
X.shape
# (100, 5)


X[:, :5]
# array([[-1.51825267, -2.28955998,  0.64205379, -2.47082997, -0.26380282],
#        [ 1.43948198,  0.91083282,  0.25170104, -0.44917451, -0.23546759],
#        [ 0.45744412, -0.06202684, -0.25803166, -1.27957377, -1.19800932],
#        [ 0.00979201,  0.51196984, -1.23243424, -1.2820214 , -0.37795672],
#        [ 3.21682083,  1.25318879,  2.34005276,  0.31735484, -1.05566578]])

7.3 Graphical LASSOの適用

Text
model = GraphicalLasso(alpha=0.2, max_iter=100)
model.fit(X)


# 推定された精度行列
Theta_est = model.precision_

7.4 結果の可視化

推定された精度行列のヒートマップを表示します。

Text
plt.figure(figsize=(6, 5))
sns.heatmap(Theta_est, annot=True, fmt=".2f", cmap="coolwarm", square=True)
plt.title("Estimated Precision Matrix (Graphical LASSO)")
plt.show()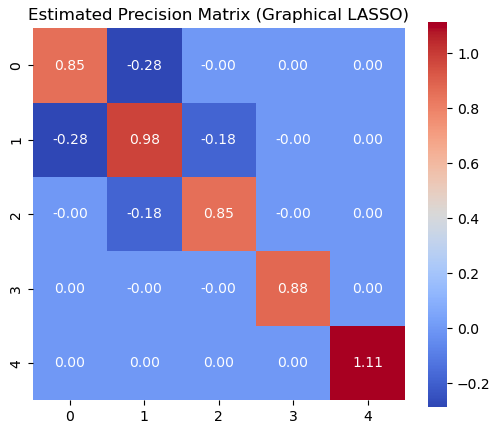

8. ハイパーパラメータの選び方

Graphical LASSOにおける重要なパラメータは正則化パラメータ λ=α\lambda = \alpha です。

この値を大きくするとスパース性が強まり、より多くの要素がゼロになります。

一方で、値を小さくするとより密な推定結果になります。

α\alpha のチューニングには以下のような方法があります。

  • **交差検証（Cross-Validation）**を用いる

  • BICやAICを基準にモデル選択

  • ドメイン知識に基づく設定

例: sklearn.covariance.GraphicalLassoCV クラスを用いると自動でα\alphaのチューニングが可能です。

Text
from sklearn.covariance import GraphicalLassoCV


model_cv = GraphicalLassoCV()
model_cv.fit(X)
print("Optimal alpha:", model_cv.alpha_)

9. 遺伝子発現ネットワークの構造推定の例

以下は、ある転写因子のmRNA量をその他の転写因子の線形結合でモデル化しLASSO等を用いて係数を決め、各転写因子をノードに係数をエッジの重みとしたグラフになります。

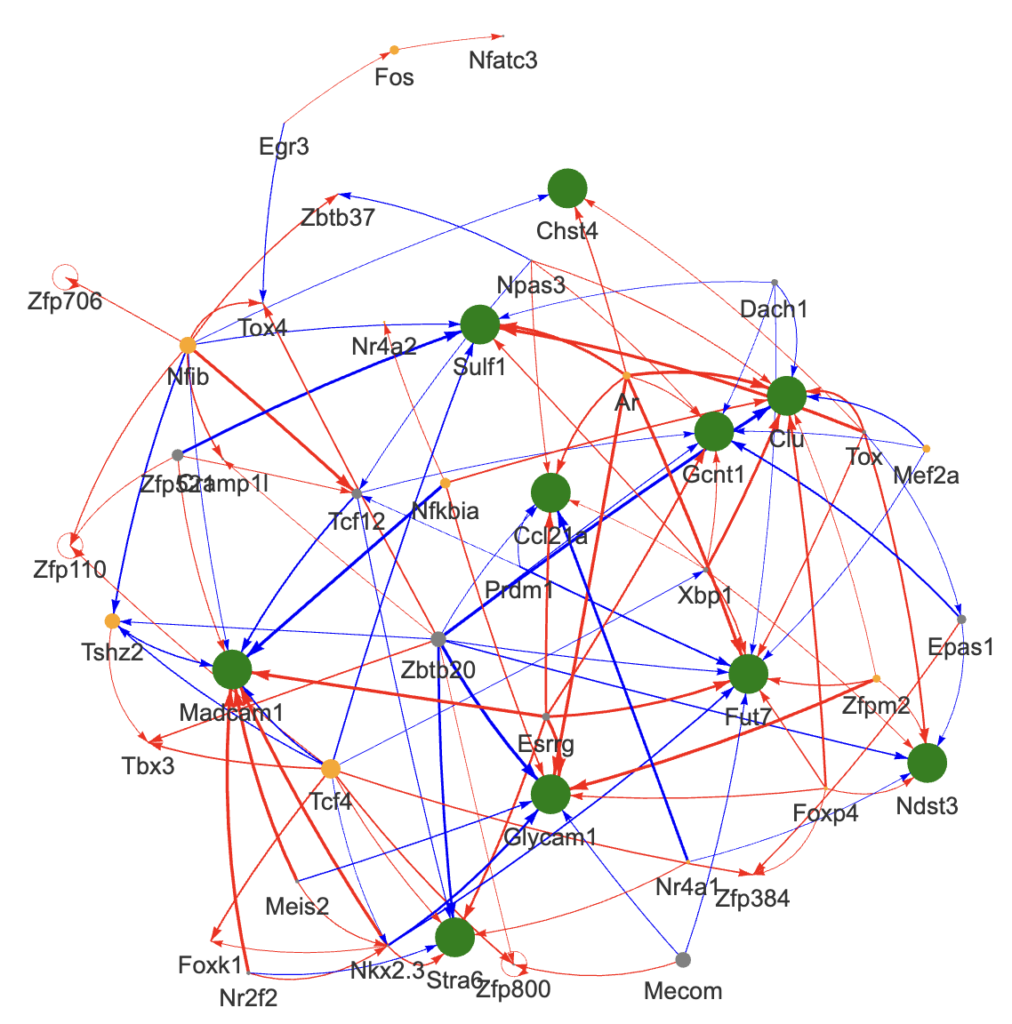
当然この方法では、間接的な制御が直接的な制御としても現れます。

例えば、A → B → Cという制御であった場合、A → B → Cというエッジに加え、A → Cというエッジも現れます。

この間接的なみかけの制御を排除するためにGraphical LASSOを利用してみます。

9.1. 入力データ

列に転写因子、行に細胞が対応する二次元データを用意します(ii列目のjj行目は転写因子iiのjj番目の細胞におけるmRNA量となるようなテーブルデータ)。

Text
import pandas as pd


# 以下は例
df_X = pd.DataFrame([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
df_X.columns = ['Ar', 'Esrrg', 'Nr2f2']
df_X.index = ['cell1', 'cell2', 'cell3']
df_X
ArEsrrgNr2f2
cell1123
cell2456
cell3789

9.2. Graphical LASSOの実施と相関行列の作成

Text
# np.arrayに変換
X = np.array(df_X)


# GraphicalLassoCV を実行する。
model = GraphicalLassoCV(alphas=4, cv=5)
model.fit(X)


# 分散共分散行列を取得する。
# -> 参考URL：https://scikit-learn.org/stable/modules/generated/sklearn.covariance.GraphicalLassoCV.html
covariance_matrix = model.covariance_


# 分散共分散行列を相関行列に変換する。
diagonal = np.sqrt(covariance_matrix.diagonal())
correlation_matrix = ((covariance_matrix.T / diagonal).T) / diagonal

9.3. 見かけのエッジリストを作成

Text
# グラフ表示のために対角成分が0の行列を生成する。
correlation_matrix_diag_zero = correlation_matrix - np.diag(np.diag(correlation_matrix) )
df_grahp_data = pd.DataFrame(index=genes, columns=genes, data=correlation_matrix_diag_zero.tolist())


# negative listを作成
negative_list = []
for i in range(len(df_grahp_data)):
  for j in range(i + 1, len(df_grahp_data)):
    if abs(df_grahp_data.iloc[i, j]) < cutoff:
      negative_list.append([genes[i], genes[j]])

9.4. 見かけのエッジを除去したグラフの描画

Text
# 1. フィルター前のエッジに関する二次元配列のデータ
# 各行が1つのエッジに対応。1列目はtargetのnode名、2列目はsourceのnode名、3列目はedgeの重さ、4列目はエッジの色
# 今回の場合、転写因子Aに対しA以外の転写因子の線形結合をXのデータを用いてLASSOでモデル化した際に係数が0でなければAがtargetで係数が0でなかった転写因子がsource
# なおその際の係数がedgeの重さで色は係数の符号に対応。
# 以下は「エッジに関する二次元配列のデータ」の例。本来は上述のようにしてXからLASSOなどで決める。
edge_list = [['Esrrg', 'Ar', 3, 'red'], ['Nr2f2', 'Ar', 2, 'blue']] # , ...]


# 2. negative_listのエッジを除く
print(f'Graphical Lasso: {len(edge_list)} --> {len(edge_list) - len(negative_list)}')
filtered_edge_list = []
for edge in edge_list:
    # filter by graphical lasso
    target = edge[0]
    source = edge[1]
    if target != source:
        if [target, source] in gl_neg_list or [source, target] in gl_neg_list:
            continue
    # add edges
    filtered_edge_list.append(edge)


# 3. ノードのリストを作成
nodes_list = []
for e in filtered_edge_list:
    nodes_list.extend([e[0], e[1]])
nodes_list = list(set(nodes_list))


# 4. dataframe化
# edges
df_edges = pd.DataFrame(filtered_edge_list, columns=["target", "source", "weight", "color"])
# nodes
df_nodes = pd.DataFrame({
	'node': nodes_list,
	'color': [ # blue_list, red_list, green_list(ノードの色)は各々で好きなように定義
		'blue' if g in blue_list else
		'red' if g in red_list else
		'green' if g in green_list else 'gray' for g in nodes_list
	],
	'size': 20
    })


# 5. グラフを描画 & 保存
# pyvisでグラフを描画
import networkx as nx
from pyvis.network import Network
# df_edgesからグラフ作成
G = nx.from_pandas_edgelist(df_edges, source="source", target="target", edge_attr=True, create_using=nx.DiGraph())
# ノードの情報を加える
node_attr_dic = df_nodes.set_index("node").to_dict(orient="index")
nx.set_node_attributes(G, node_attr_dic)
# グラフ描画
pyvis_G = Network(notebook=True)
pyvis_G.from_nx(G)
pyvis_G.show_buttons(True)
pyvis_G.show(f'filtered_network.html')

見かけのエッジを除いたところ、以下のようなすっきりしたグラフになりました。

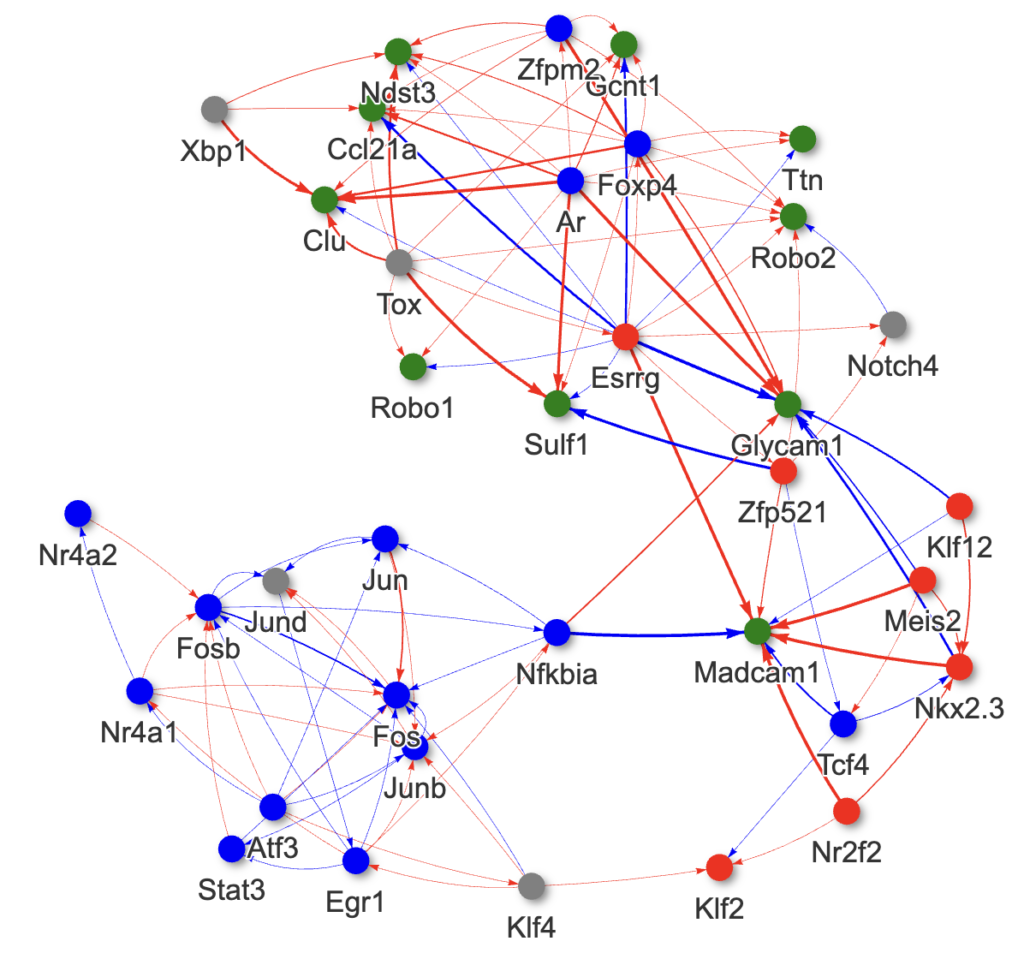
10. まとめ

Graphical LASSOは、高次元データにおける変数間の条件付き独立性を推定し、スパースなネットワーク構造を明らかにする強力な手法です。

Pythonを用いれば、sklearnライブラリで手軽に実装できるため、応用範囲は広がります。

参考文献

  • Friedman, J., Hastie, T., & Tibshirani, R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics, 9(3), 432–441.

  • Witten, D. M., Friedman, J. H., & Simon, N. (2011). Statistical learning techniques for high-dimensional data. Springer.

  • Scikit-learn documentation: GraphicalLasso